Conceptos elementales de estadística en investigación clínica: todo lo que se debe saber un neurocirujano para leer críticamente un trabajo y para reportar sus propios resultados

Título

Autor

Kevin P. White

Fecha

Marzo 2018

Texto

REV ARGENT NEUROC | VOL. 32, N°1: 41-57| 2018
ARTÍCULO DE REVISIÓN

Conceptos elementales de estadística en investigación clínica: todo lo que se debe saber un neurocirujano para leer críticamente un trabajo y para reportar sus propios resultados

Kevin P. White

Médico doctorado en Epidemiología y estadística CEO

Science Right Editing & Publishing

Tradución: Mariano Socolovsky

INTRODUCCIÓN

¿Le gustaría sentirse seguro eligiendo el test estadístico correcto para analizar sus datos? Si su respuesta es afirmativa, este trabajo ha sido escrito específicamente para usted, en especial si posee poco o ningún conocimiento sobre estadísticas biomédicas. Pero también ha sido realizado para que pueda compartir este trabajo con cualquier investigador que no posea un entrenamiento formal en el tema. Se encuentra dirigido especialmente a quienes realicen investigación clínica, aunque también puede ser utilizado por quienes realicen actividades de investigación básica en laboratorio. He tratado de hacer esto lo más claro y sencillo posible, por ello no me detendré en explicar todos los test disponibles, sino los más comúnmente utilizados, sobre todo en investigación clínica. Ellos son:

Test de la t de Student- emparejado y sin emparejar.
Análisis de varianza (ANOVA).
Prueba de Pearson chi al cuadrado (χ2).
Coeficiente Kappa de Cohen (y de Fleiss).
Análisis de la correlación.
Análisis de la regresión.
Tres pruebas no paramétricas comúnmente utilizadas:
Prueba de los rangos signados de Wilcoxen.
Prueba U de Mann-Whitney.
Prueba H de Kruskal-Wallis.

Nuevamente, el objetivo de este trabajo es enseñarle cuándo seleccionar y utilizar estos tests, pero no cómo realizarlos. También incluiré algunas reglas básicas sobre análisis. La metodología específica de cómo realizar estas pruebas dependerá del software que usted se encuentre utilizando (SPSS, SAS, Minitab, etc.).

¿POR QUÉ REALIZAR UN ANÁLISIS ESTADÍSTICO?

Existen muchas razones, siendo las más frecuentes en investigación clínica:

Realizar comparaciones entre grupos
El primer objetivo extremadamente común de las pruebas estadísticas en ensayos clínicos o encuestas es comprobar si dos o más grupos son estadísticamente diferentes, en términos de un valor/característica basal dado o resultado posterior al tratamiento. Estos grupos pueden ser pacientes que reciben diferentes tratamientos (por ejemplo, un fármaco activo versus placebo o cirugía versus ninguna cirugía) o personas con alguna otra característica distintiva (por ejemplo, edad <40 versus 40-59 versus ≥ 60 años).
Realizar comparaciones dentro de un mismo grupo
Un segundo objetivo muy común de las pruebas estadísticas es comparar una medida particular realizada más de una vez. Un ejemplo es cuando dos o más observadores realizan una medición, para ver cuán cerca están de acuerdo, en promedio, las mediciones. Otro ejemplo son las mediciones múltiples a lo largo del tiempo; por ejemplo, se podría probar si los pacientes experimentan una reducción estadísticamente significativa en la gravedad de un síntoma o marcador de enfermedad dado a lo largo del tiempo: como en la comparación de la gravedad del dolor después de haber recibido determinado tratamiento farmacológico o procedimiento quirúrgico, en relación al estado previo a recibir dicho tratamiento.

Tenga en cuenta que, para la mayoría de los ensayos clínicos (si no todos), sería prudente realizar comparaciones entre grupos y dentro de un mismo grupo. Por ejemplo, si desea saber si un medicamento dado es más eficaz que el placebo para reducir la gravedad del dolor de un paciente, es probable que desee realizar comparaciones entre grupos de estos dos grupos de pacientes (fármaco activo versus placebo) para ver cómo los dos grupos se comparan con respecto a sus características iniciales y sus resultados finales. Sin embargo, también es posible que desee realizar comparaciones dentro del grupo para ver si algún sub-grupo mejora estadísticamente o empeora con el tratamiento, en comparación con el dolor pre-tratamiento.
Qué tal de hacer ambas cosas al mismo tiempo: ¿no sólo ver si un grupo cambia frente a la línea de base, sino también si dos subgrupos son diferentes en su grado de cambio desde el inicio? Una forma en que puede hacer esto es ver si un solo subgrupo cambia estadísticamente frente a la línea de base, mientras que el otro no lo hace. Pero esto, de hecho, NO significa que los dos grupos sean estadísticamente diferentes en su grado de mejora. Un ejemplo de esto se puede ver en la Figura 1. En este ejemplo, el dolor disminuye gráficamente en ambos grupos, con las dos líneas casi paralelas. Sin embargo, la diferencia entre el seguimiento inicial y final SOLO alcanza significación estadística para el fármaco activo, y simplemente no logra una significación estadística límite (la significación estadística límite se considera a menudo p entre 0,05 y 0,10) para el placebo. ¿Podría alguien decir, con confianza, que este fármaco activo particular es mejor que el placebo?
A menos que los dos grupos de tratamiento comiencen exactamente con el mismo nivel de dolor, simplemente comparar el nivel de dolor en el seguimiento final también sería poco útil, ya que esto no reflejaría el cambio en el dolor a lo largo del tiempo, como se muestra en la Figura 2 (abajo). De nuevo, las dos líneas que indican el cambio son casi paralelas. La única razón por la cual el nivel promedio de dolor fue diferente en los dos grupos en el seguimiento final es porque los dos grupos también fueron bastante diferentes al inicio (aunque, una vez más, no lograron alcanzar la significación estadística límite).
Lo que debe hacer para realmente dilucidar este problema es combinar de alguna manera las diferencias entre grupos y dentro de un grupo en una sola prueba. Una forma de hacerlo sería creando una nueva variable, llamada 'cambio desde la línea de base', que calcule el nivel de dolor al final del seguimiento MENOS el nivel de dolor al inicio del estudio. Para los datos de la Figura 1, estaría comparando un cambio de -34,7% en el grupo de fármaco activo frente a un cambio de -26,5% en el grupo de placebo. Para los datos en la Figura 2, estaría comparando -31.1% contra -26.5%. En ambos casos, se llegaría a la conclusión de que, a pesar de que el cambio desde el inicio fue estadísticamente significativo para el fármaco activo, pero no el placebo (fig. 1); o el nivel final de dolor fue estadísticamente menor con el fármaco activo que con el placebo en el seguimiento final (fig. 2): realmente no hubo una diferencia estadísticamente significativa en la efectividad de los dos tratamientos, es decir no fue mejor el tratamiento que el placebo.
Pero debemos tener cuidado: también es posible que dos tratamientos (por ejemplo, cirugía y placebo) puedan ser estadísticamente diferentes entre sí, incluso cuando ninguno de los produzca una mejora significativa y tampoco haya una diferencia significativa en el resultado de interés, ya sea al inicio o durante el seguimiento. ¿Cómo? Debido a que los pacientes con uno u otro tratamiento en realidad hayan empeorado, como se muestra en la Figura 3.
En la figura 3, hay una leve mejoría en los pacientes con tratamiento activo versus placebo, pero no lo suficiente como para acercarse a la significación estadística. Hay un ligero empeoramiento con el placebo, pero, nuevamente, no lo suficiente como para ser estadísticamente significativo. Y no hay diferencias intergrupales estadísticamente significativas en el resultado de interés en el seguimiento inicial o final. Sin embargo, existe una diferencia superior al 25% entre los dos grupos de tratamiento en el porcentaje de cambio entre el inicio y el seguimiento final (un aumento del 11% frente al 14% de reducción del dolor), que podría ser estadísticamente significativo.

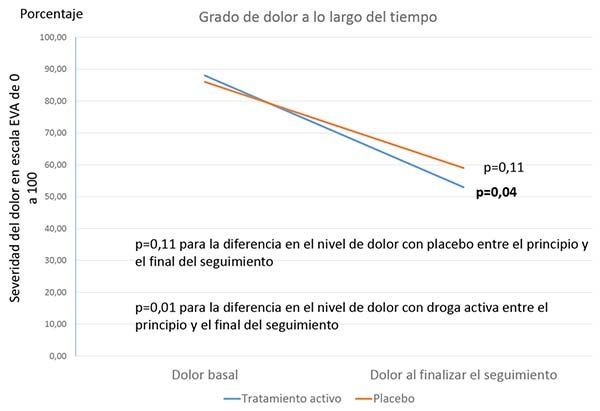
Figura 1.

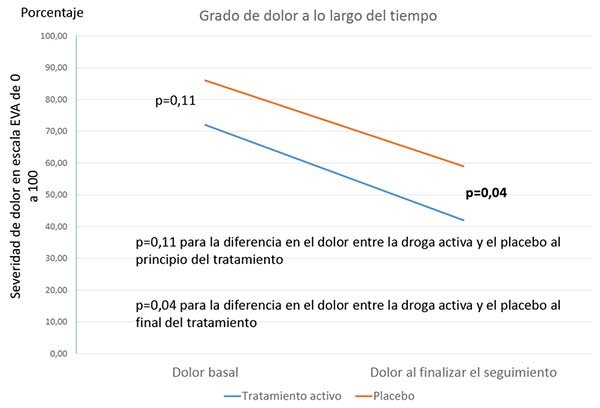
Figura 2.

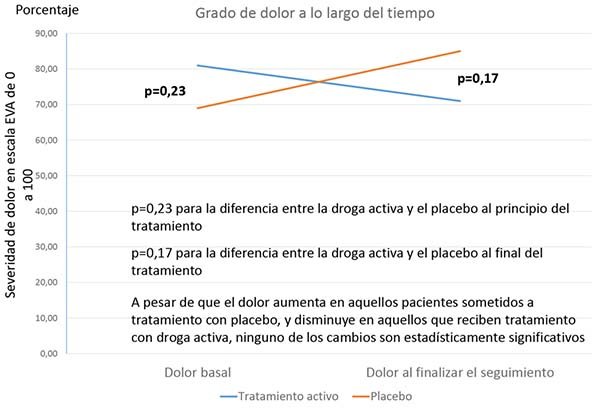
Figura 3.

En este último ejemplo, entonces, la única forma de mostrar que un tratamiento fue mejor que el otro es observar el cambio desde el inicio hasta el seguimiento final, en este caso y como ya se ha explicado, creando una variable que abarque el porcentaje de cambio en el resultado de interés entre los puntos de referencia y de seguimiento final. En este punto conviene definir qué es una variable estadística: se trata de un conjunto de valores que puede tomar cierta característica de la población sobre la que se realiza un determinado estudio estadístico y sobre la que es posible su medición. Estas variables pueden ser: la edad, el peso, las notas de un examen, los ingresos mensuales, las horas de sueño de un paciente en una semana, el precio medio del alquiler en las viviendas de un barrio de una ciudad, etc.
Más adelante, le mostraré una forma aún MEJOR de hacer esto (detectar cambios estadísticamente significativos). Sin embargo, el punto que quiero resaltar ahora es:

Regla #1: En los ensayos clínicos o en cualquier estudio prospectivo en el que se sigan grupos de sujetos a lo largo del tiempo, realizar comparaciones entre grupos y dentro del grupo a menudo conduce a una comprensión mucho mejor de la "verdad" que realizar sólo una de las dos formas de comparación en forma aislada.

Dicho esto, es crucial entender que la prueba de que dos grupos o dos valores a lo largo del tiempo son estadísticamente diferentes es solo la mitad de la historia. Lo que también es importante es si las diferencias estadísticamente significativas detectadas también son clínicamente significativas. Por ejemplo, imagine que existe una enfermedad particular que se considera 100% fatal en un año, a pesar del tratamiento. Ahora imagine a un paciente que recibe el medicamento A y que permanece con vida tres años después del diagnóstico. La supervivencia altamente imprevista de este paciente es claramente de importancia clínica; pero no puede ser probada estadísticamente, ya que solo hay uno de esos pacientes. Si usted fuera el médico de ese paciente, ¿podría negar seriamente darle a su próximo paciente con la misma enfermedad la opción de ese mismo medicamento? De hecho, ha habido casos en los que un número muy pequeño de éxitos de tratamiento o fallas catastróficas han resultado en que las juntas de revisión ética se nieguen a aprobar incluso un solo estudio pequeño y controlado que implique el tratamiento implicado, alegando razones de índole ética.
De manera similar, si, como parte de una gran encuesta, se determinara que hubo una diferencia estadísticamente significativa de sólo un uno por ciento en la tasa de supervivencia a un año entre los pacientes que recibieron un medicamento versus otro, ¿podría recomendar encarecidamente ese primer medicamento como "superior" a sus pacientes? Estadísticamente, sí, quizás. Pero clínicamente, están lo suficientemente cerca como para que otros factores, como el costo y los efectos secundarios, tengan un papel más importante en la toma de decisiones que la "superioridad" del 1% de un medicamento.
En consecuencia, mi segunda regla de análisis estadístico es:

Regla #2: La significancia estadística y la significancia clínica son AMBAS importantes.

En otras palabras, para que un hallazgo de investigación determinado se considere significativo, en la mayoría de los casos debe ser TANTO clínicamente como estadísticamente significativo. Reconozcamos que, casi CUALQUIER ensayo que sea lo suficientemente grande encontrará una diferencia estadísticamente significativa entre grupos. Sin embargo, demostrar que un tratamiento tiene un beneficio estadísticamente significativo, pero que carece de importancia clínica sobre otro, en sí mismo no tiene sentido y no tiene fundamento. Es por eso que a veces me estremezco cuando escucho a la gente decir: "Si el estudio SÓLO hubiera sido un poco más grande, podríamos haber encontrado algo". Los investigadores que saben lo que están haciendo deciden de antemano qué diferencia es necesaria para que sea clínicamente significativa, y ulteriormente diseñan sus estudios para que sean lo suficientemente grandes como para detectar esa diferencia.
No obstante, lo considerado más arriba, debido a que ésta es una introducción al análisis estadístico básico, el resto del presente trabajo será dedicado a analizar la significación estadística y no la clínica.

¿QUÉ SE PUEDE COMPARAR?

Al realizar un análisis estadístico, ya sea que se esté comparando diferentes grupos o las mediciones recopiladas de uno o más grupos a lo largo del tiempo, lo que se puede comparar realmente es:

Valores promedio
Por ejemplo, ¿la presión arterial sistólica (PAS) media en un grupo de pacientes es diferente a la PAS media en otro grupo? Tenga en cuenta que la presión arterial sistólica es un valor continuo (en otras palabras, hay una escala continua de presión arterial, que varía desde un mínimo de tal vez 80 hasta un máximo de quizás 180, con cada valor posible).
Si creara una tabla para describir los dos grupos, podría verse más o menos así:

Grupo A

Grupo B

Presión sistólica promedio

145.7 mmHg

153.2 mmHg

Los promedios se pueden comparar cuando los valores potenciales de una variable particular de interés son (1) continuos (p. Ej., De 0 a 100) y (2) distribuidos normalmente (lo que significa que, cuando se trazan en un gráfico, se visualizan aproximadamente como una campana (fig. 4).
La proporción de una variable versus otra
Por ejemplo, qué porcentaje de mujeres frente a hombres tiene una presión arterial sistólica alta, definida como PAS ≥ 140. Tenga en cuenta que, aunque la presión arterial es una variable continua, aquí se trata como un binomio (cualquier valor PAS ≥ 140 versus cualquier valor PAS <140). La presión arterial (PA) de cada paciente es "alta" o "no alta". Si creó una tabla para describir los dos grupos, se vería algo así como mostrando el número (y porcentaje) de sujetos en cada grupo con una PAS alta versus una normal:

Mujeres, n (%)

Hombre, n (%)

PAS normal

45 (75.0%)

32 (53.3%)

PAS elevada

15 (25.0%)

28 (46.7%)

Los rangos de un valor o medida particular
En lugar de comparar las presiones sanguíneas promedio o la proporción con presiones sanguíneas altas versus normales, también se podría desear clasificar la presión arterial en rangos de valores. Por ejemplo, si las presiones sanguíneas sistólicas en el Grupo A son, de mayor a menor, 183, 162, 150, 145, 138, 128, 110 y 108; y en el Grupo B 185, 178, 152, 146, 126, 125, 114 y 106, tendría una tabla que se vería así, con los rangos relativos de estas medidas entre paréntesis:

Grupo A PAS (rango)	Grupo B PAS (rango)
183 (2)	185 (1)
162 (4)	178 (3)
150 (6)	152 (5)
145 (8)	146 (7)
138 (9)	126 (11)
128 (10)	125 (12)
110 (14)	114 (13)
108 (15)	106 (16)

Tenga en cuenta que el Grupo B tiene presiones sanguíneas que son la 1º más alta, la 3ª más alta, la 5ª más alta, la 7ª más alta, la 11ª a la 13ª más alta y la 16ª más alta.
Las pruebas de rango se utilizan en el análisis cuando los valores medidos para la variable de interés no se distribuyen normalmente entre los grupos de estudio (no hay una curva en forma de campana), ya que una distribución en forma de campana es una suposición esencial de todas las llamadas pruebas paramétricas.
Las pruebas de rango no son paramétricas, lo que las hace algo más conservadoras (menos sensibles a las diferencias de detección) que las pruebas paramétricas, compensando de ese modo la incertidumbre relativa asociada con los datos no distribuidos normalmente (discutidos más adelante). Por esta razón, las pruebas no paramétricas generalmente NO se deben usar en datos distribuidos normalmente, ya que su análisis será propenso a perder verdaderas diferencias entre los grupos.
Por ello, mi tercera regla para el análisis estadístico es:

Regla #3: Si los valores de medición de una variable continua de interés (por ejemplo, presión sanguínea) están normalmente distribuidos (es decir, forman aproximadamente una curva en forma de campana), use pruebas paramétricas. Si no lo son, use pruebas no paramétricas (por ejemplo, rango).

Figura 4.

COMPRENDIENDO SUS VARIABLES

Antes de poder determinar cuál es la mejor prueba estadística que debe utilizar en su trabajo de investigación, usted debe comprender y clasificar las variables que posee, en relación a seis puntos que se desarrollan a continuación y que son: variables dependientes, variables independientes, variables continuas, variables categóricas, variables nominales; y variables ordinales.
Teniendo estos puntos en cuenta, hay esencialmente dos preguntas que Ud. se deberá hacer sobre cada una de sus variables de datos antes de utilizarlas en su análisis:

¿Usted está intentando usar una variable como variable dependiente o independiente?
¿Su variable es continua, ordinal o nominal?

¿Su variable es dependiente o independiente?
Comencemos definiendo estos términos:
Variable dependiente: Esta es la variable más importante que usted está midiendo. En el ejemplo anterior sobre presión arterial sistólica, su variable dependiente será la presión sistólica misma, ya que usted estaba comparando mediciones de la presión sistólica entre diferentes grupos de pacientes
Variable independiente: Esta es la variable que define los diferentes grupos que usted está estudiando. En el primer y el tercer ejemplo, la variable independiente era “Grupo” (Grupo A versus Grupo B); en el segundo ejemplo, la variable era “Sexo” (masculino-femenino).
Los análisis generalmente requieren la existencia tanto variables dependientes como de independientes. Por ejemplo, si usted quiere saber si los pacientes con Glioblastoma Multiforme sometidos a resección tumoral subtotal viven más tiempo que aquellos que no son operados, la variable dependiente será tiempo de sobrevida (medida en las unidades que Ud. desee: días, semanas, meses, años), mientras que la variable independiente será grupo de tratamiento (resección subtotal versus no operados).
Es importante mencionar que una variable puede ser utilizada como dependiente en un análisis y como independiente en otro. En otras palabras, usted el hecho de que una variable determinada sea dependiente o independiente dependerá enteramente de su elección.
Para ilustrar esto, podemos tomar los tres ejemplos descriptos anteriormente sobre presión arterial sistólica (PAS). En ellos tres, en los tres, la PAS fue la variable dependiente. Pero usted también puede preguntar con los mismos datos: ¿es la PAS un predictor de accidente cerebrovascular hemorrágico (ACVH)? En este caso, la “presencia o ausencia de ACVH será la variable dependiente -la de mayor interés- mientras que la PAS será su variable independiente.

¿Son sus variables continuas, ordinales o nominales?
Ahora, tanto sean utilizadas como dependientes o independientes, todas las variables, por su misma naturaleza, serán continuas, ordinales O nominales.
Variables continuas: Una variable continua es aquélla en la cual los valores numéricos potencialmente obtenidos son continuos: por ejemplo, en la PAS, serán mediciones en mmHg; o mediciones de la altura en centímetros, o del peso en Kg.; o el nivel de dolor que posee un paciente, determinado por ejemplo en la escala visual análoga de 0 a 100, donde cero es nada de dolor y 100 es dolor máximo.
Una segunda característica distintiva de las variables continuas es que la relación entre los valores posibles permanece constante a medida que se incrementan los mismos; en otras palabras, si por ejemplo vamos a utilizar la escala visual análoga 0-100 para cuantificar severidad de dolor, la distancia entre 10 y 11 será la misma que entre 45 y 46, o 79 y 80, etcétera. Por lo tanto, es apropiado resumir los resultados obtenidos de la cuantificación de variables continuas, mediante el promedio.
Si una variable cumple con estos dos criterios, esencialmente es continua. Note que no debe tener un número infinito -ni siquiera grande- de opciones. Si usted le pregunta a alguien cuántos días por semana se cepilla los dientes, y le da la posibilidad de responder de cero a siete, ESO es esencialmente una variable continua. Sin embargo, si usted posee una variable con 5 o menos opciones -por ejemplo, el número de días fuera del fin de semana, en que realiza ejercicio- muchos coinciden en que esa variable debe ser tratada como ordinal, aún si cumple los dos criterios antes mencionados. ¿Por qué es eso? No lo sé; pero podría tener que ver con la baja posibilidad existente de normalizar los datos, y la consiguiente pérdida de poder de análisis estadístico si se analizan datos no distribuidos normalmente con pruebas para datos normalizados (este tema se desarrollará un poco más adelante).
Las dos categorías remanentes, variables nominales y ordinales, se colocan debajo del paraguas de las variables categóricas. Contrariamente a las variables continuas, las categóricas son aquellas en las cuales los datos son asignados a diferentes categorías, las cuales pueden poseer o no un rango lógico.
Las más sencillas de comprender son las variables nominales.
Variables nominales: son las que no poseen un orden lógico de categorías. Por ejemplo: masculino versus femenino; Grupo A recibiendo discectomía lumbar percutánea versus Grupo B recibiendo cirugía placebo; Raza Blanca versus Amarilla versus Negra versus Otras. En cada caso, se asume que no hay un grupo mejor que otro. Esto también es cierto aún si usted asigna a cada categoría un número para facilitar el análisis (por ejemplo; 0= sin diabetes, 1=diabetes juvenil, 2=diabetes del adulto, 3=diabetes gestacional, 4= otras).
Las variables ordinales son un poco más complicadas, ya que se puede tender a confundirlas con las continuas, y rotularlas de esta manera. Sin embargo, es crucial que no lo haga. Veamos:
Variables ordinales: Una variable ordinal es aquella en la cual
A cada sujeto se le asigna un valor o calificación que abarca un rango de mediciones individuales; y
Hay un orden lógico para esos valores.
Por ejemplo, si clasifica la presión arterial sistólica en el nivel 1: PAS <140; nivel 2: PAS entre 140 y 159; nivel 3: PAS entre 160 y 179; y nivel 4: PAS ≥ 180, está usando una escala ordinal, con cada sujeto recibiendo una calificación de PAS de entre uno y cuatro. Por lo tanto, si la PAS de un sujeto determinado es 145, se asignarían a la categoría 'PAS entre 140 y 159', y se le asignaría el valor de '2'; si su PAS es 182, se les asignaría un valor de '4'. Tenga en cuenta que no tiene sentido calcular un valor promedio para una escala ordinal como ésta, ya que es concebible que, en un grupo de sujetos, un porcentaje desproporcionadamente alto pueda tener una PAS en el rango inferior de un cierto nivel mientras que, en el otro grupo, lo contrario podría ser cierto y estar cerca del rango superior. Calcular los promedios de PAS de cada grupo sería, por lo tanto, bastante engañoso y, por ende, no interpretable.
Asimismo, es posible dividir la edad de un paciente de la misma manera; por ejemplo,

Pacientes menores de 20 años;
Pacientes de 20 a 39 años de edad;
Pacientes 40-59;
Pacientes 60-79; y
Pacientes> 80 años de edad, clasificando la edad en una escala de 1 a 5. De hecho, CUALQUIER variable continua se puede subcategorizar en una escala ordinal, SI elige hacer esto.

Efectivamente, existen casos en los que convertir una variable continua en una ordinal podría ser de interés:

Identificar un valor umbral: la primera instancia podría ser cuando desee identificar algún valor de corte o umbral en el que algo cambia. Por ejemplo, demostrar estadísticamente que el riesgo de accidente cerebrovascular de una población determinada aumenta a medida que aumenta su PAS sería de utilidad, pero no le dice cuándo comenzar a reducir la presión arterial de un paciente. Por otro lado, determinar que la incidencia de ACV se duplica cuando la PAS alcanza 140 mmHg SI ayuda a decidir cuándo iniciar el tratamiento. En el mismo estudio en el que usted demostraría que el riesgo de accidente cerebrovascular aumenta con el aumento de la PAS (como una variable continua), usted también puede convertir su escala PAS continua en una escala ordinal; por ejemplo, 1=PAS <120 mmHg; 2=PAS 120-139 mmHg; 3=SBP 140-159 mmHg; y así. Si la incidencia de accidente cerebrovascular es más o menos la misma en los grupos 1 y 2, pero se duplica en el grupo 3 y continúa aumentando en los grupos subsiguientes, esto sugiere que 140 mmHg es un nivel de PAS al que puede ser aconsejable iniciar el tratamiento.
Cuando la respuesta dada es una estimación: una segunda razón para convertir una escala continua en una escala ordinal es cuando el valor que está analizando es estimativo. Por ejemplo, si le pregunta a alguien cuál es su ingreso anual y le responde $35,000, probablemente no sea EXACTAMENTE $35,000. Lo más probable es que su salario sea APROXIMADAMENTE $35,000. Esto es muy diferente al nivel de precisión al que esperaría medir la presión arterial sistólica de una persona. Por esta razón, tiene mucho más sentido asignar diferentes sujetos a diferentes rangos de ingresos anuales (por ejemplo, <$20,000; $20-39,000; $40-59,000... etc.) antes de realizar cualquier análisis que utilice esta variable.

¿Puede la inversa también ser cierta? ¿Se puede convertir una escala ordinal en una continua? No me refiero a volver a convertir una escala ordinal en una escala continua cuando ya posee los datos continuos: como convertir la PAS en categorías, pero luego volver a utilizar los datos continuos previamente obtenidos para ciertos análisis posteriores. Me refiero verdaderamente a convertir una escala ordinal en una continua.
Por ejemplo, en una encuesta de población muy grande, usted puede asignar valores de 1 a 12 a individuos en función de su nivel de educación, con 1=no terminó la escuela primaria; 2=terminó la escuela primaria; 3=no terminó la escuela secundaria; 4=graduado de la escuela secundaria; 5 no se graduó en la universidad; 6=graduado en la universidad; 7=no terminó un post-grado; 8=tiene título de post-grado... hasta 12, que sería un doctorado.
Dado que esta escala posee clasificaciones potenciales continuas de 1 a 12, ¿podría considerarse como una escala continua? Brevemente, la respuesta es NO. He aquí el porqué:
Recuerde que una de las características esenciales de cualquier variable continua es que la relación entre valores sucesivos siempre permanezca igual. Lo que esto significa es que, para cualquier escala que comience en 0 o 1, el valor medio de la categoría "2" DEBE ser exactamente el doble del valor medio de la categoría "1"; el valor medio de la categoría '3' DEBE ser exactamente tres veces el valor medio de la categoría '1'; el valor medio de la categoría '4' debe ser exactamente 4 veces el valor medio de la categoría '1' y exactamente el doble del valor medio de la categoría '2'; y así sucesivamente.
No obstante, en el ejemplo anterior, ¿puede usted con seguridad llamar completar la escuela primaria (calificación=2) exactamente el doble del valor de no terminar la escuela primaria (calificación=1)? ¿Puedes llamar tener un título de post-grado (calificación 8) exactamente el doble del valor de completar la escuela secundaria (calificación 4)? La respuesta a ambas preguntas es no. Claramente, tener un diploma de escuela secundaria significa tener más años de educación formal que simplemente haber completado la escuela primaria, pero de cuánto más valor uno tiene en relación con el otro solo se puede especular, y por supuesto varía de individuo a individuo.
¿Y cómo podría interpretar un valor promedio de, por ejemplo, 5.9? ¿Eso significa que la persona promedio en su muestra tiene un nivel medio de educación apenas por debajo de un título universitario? Claramente, tal interpretación sería inapropiada.
Este problema que se presenta al convertir una variable ordinal en una continua es aún más obvio si las respuestas disponibles son algo así como:

más de una vez al día,
≤una vez por día,
≤una vez por semana,
≤una vez al mes, o
≤una vez al año.

En este segundo ejemplo, no solo cada respuesta es una estimación dentro de un rango, sino que el tamaño de cada categoría varía enormemente: desde un día para las opciones de respuesta (1) más de una vez al día y (2)≤una vez por día, hasta 365 + días para la opción de respuesta (5)≤una vez al año.
Por lo tanto, cuando usted analice una escala ordinal que simplemente estime la frecuencia de un síntoma o evento dado, como éste (en categorías amplias), no tiene sentido considerarlo continuo, sin importar cuántas calificaciones potenciales haya.
Para resumir lo explicado hasta aquí para las clasificaciones de las variables, en la tabla 1 encontrará varios ejemplos de cada tipo de variable.
Espero que, con todo esto, haya logrado aclarar este tema. La razón por la que le he dedicado un espacio considerable es que resulta crucial conocer que las pruebas diseñadas para variables continuas no deben, en la mayoría de las circunstancias, usarse para escalas ordinales, incluso cuando la escala ordinal involucra una gran cantidad de números aparentemente continuos.

Regla # 4: las variables continuas PUEDEN convertirse a escalas ordinales, y algunas veces esto es útil. EN MUY RARAS OCASIONES, es posible convertir con la seguridad suficiente, una escala ordinal en una que sea continua.

La quinta regla es la causa de toda la sección actual, y da pie para todo lo que sigue a continuación:

Regla # 5: Para determinar qué prueba se debe utilizar, debe considerar si su variable dependiente es continua, nominal u ordinal; y luego hacer lo mismo con su variable independiente.

La tabla 2 es fundamental, ya que permite determinar cuál es la prueba estadística que requieren sus datos para ser correctamente analizados.

COMPRENDIENDO LAS PRUEBAS

Tabla 1: Ejemplos de variables nominales, ordinales y continuas

Tipo de variable	Ejemplo
Nominal	Género; Raza; País de origen.
	Grupo de tratamiento (por ejemplo, tratamiento activo frente a placebo).
	Estado de empleo: a tiempo completo, a tiempo parcial; estudiante; desempleado; retirado; otro.
	Diabetes (sí/no); Sobrevida (sí/no).
	Resultado a los 30 días de seguimiento: muerte; permanece hospitalizado; dado de alta.
Ordinal	Nivel de satisfacción con el tratamiento: 1=muy insatisfecho; 7=muy satisfecho.
	Años de trabajo: cero-5; 6-10; 11-15; 16-20; más de 20.
	Dosis de la medicación: cero (placebo); 5 mg/día; 10 mg/día; 20 mg/día.
	Número de niños: 1, 2, 3, 4, 5 o más.
	¿Con qué frecuencia lees un libro de ficción? Nunca; De vez en cuando; A menudo; A diario.
Continua	Presión arterial sistólica en una escala continua.
	Edad en años; Meses de embarazo; Edad gestacional (en semanas).
	Promedio de días por mes que sale de la ciudad.
	Recuento de linfocitos promedio por campo microscópico.

Tabla 2: Eligiendo la prueba correcta para sus datos

		Variable dependiente
Variable independiente	Nominal	Ordinal	Continua
Nominal	Prueba de Pearson chi al cuadrado (χ2). Coeficiente Kappa de Cohen.	Prueba de Pearson chi al cuadrado (χ2). Pruebas de rangos no-paramétricos (si son 2 grupos: prueba de los rangos signados de Wilcoxen, o prueba U de Mann-Whitney) (si > 2 grupos, prueba H de Kruskal Wallis).	Prueba de la t de Student (si son 2 grupos). ANOVA (si > 2 grupos). Pruebas de rangos no-paramétricos.
Ordinal	Prueba de Pearson chi al cuadrado (χ2).	Prueba de Pearson chi al cuadrado (χ2). Pruebas de rangos no-paramétricos (prueba H de Kruskal Wallis).	Prueba de la t de Student (si son 2 grupos). ANOVA (si > 2 grupos). Pruebas de rangos no-paramétricos.

Tabla 3: Pruebas estadísticas y sus estadísticos de prueba

Prueba estadística	Estadístico de prueba	Símbolo	Rango posible
Prueba de la t de Student	t	t	Cualquier valor + o –
Prueba de Pearson χ2	Chi cuadrado (χ2)	χ2	Cualquier valor positivo
Análisis de la varianza (ANOVA)	Valor F	F	Cualquier valor positivo
Análisis de la correlación de Pearson	Coeficiente de correlación de Pearson	r	-1.00 a +1.00
Análisis de la regresión	Coeficiente de regresión	β (o R)	Cualquier valor + o –

El objetivo principal de prácticamente todas las pruebas enumeradas anteriormente y que se describen a continuación es calcular un número que luego se puede utilizar para estimar la probabilidad de que una hipótesis específica sea verdadera; por ejemplo: ¿son los valores promedios de una variable específica diferente entre dos o más grupos? ¿El valor promedio de una medida específica cambió con el tiempo? El número que se calcula con cada prueba estadística se denomina "estadística de prueba" y cada prueba tiene su propio estadístico de prueba específica. Un estadístico de prueba es una variable aleatoria que se calcula a partir de datos de muestra y se utiliza en una prueba de hipótesis. Para las pruebas t de Student, por ejemplo, el estadístico de prueba es el 'valor t'. Para el análisis de Pearson χ2 (chi cuadrado), es el valor de χ2. Para ANOVA, es la 'estadística F'; y así sucesivamente. A continuación, hay una tabla corta (Tabla 3) que enumera las pruebas más comunes y la estadística de prueba que genera cada prueba.
Tenga en cuenta que todos los estadísticos de prueba se calculan no sólo en función de los valores medidos, sino también del número de sujetos, el grado de varianza entre las mediciones, los valores que se esperarían si los distintos grupos fueran idénticos, y así sucesivamente. Para algunas pruebas, el cálculo manual es posible, aunque tedioso (p. Ej., Pruebas t de Student, análisis Pearson χ2). Sin embargo, es virtualmente imposible para otros (por ejemplo, análisis de regresión). Todas estas estadísticas de prueba se calculan automáticamente con un clic del mouse dentro de una larga lista de programas de software estadísticos, que incluyen los tres programas que aprendí durante mis estudios de doctorado: SPSS, SAS y Minitab. De los que aprendí, creo que SPSS es el más fácil de usar; pero debo admitir que no he usado SAS o Minitab en más de una década, por lo que ahora pueden ser mucho más amigables para el usuario. No puedo comentar mucho más al respecto.
Si está considerando adquirir un programa de software estadístico para usted o su equipo de investigación, puede encontrar una lista (con clasificaciones de 1 a 5 estrellas) de todos los programas de software estadístico más importantes actualmente disponibles en https://www.capterra.com/statistical. -analysis-software /. Sin embargo, además de revisar esa página, le RECOMIENDO que averigüe qué están utilizando sus colegas y/o colaboradores (potenciales), ya que el hecho de que utilicen el mismo programa pueden ser de gran ayuda, y en ocasiones imprescindible. Los archivos de datos a veces se pueden convertir de un programa a otro, pero no siempre de manera directa o sencilla.
Cualquier estadístico de prueba que calcule se usa para determinar un valor p, utilizando una tabla de valores p para cada valor dado; en programas de software de estadísticas, esto se hace automáticamente. Lo que sigue son breves descripciones de las pruebas que son, con mucho, las más utilizadas.

Prueba de Pearson χ2
La prueba Pearson χ2 (también llamada análisis de Pearson chi-cuadrado) se usa siempre que construya una tabla de 2 por 2 (2 x 2) como la siguiente, donde tanto la variable dependiente como la independiente sean nominales u ordinales. En pocas palabras, está probando si las proporciones (o porcentajes) de sujetos en las distintas "células" son los mismos en los dos grupos.

	Mujeres (número, n =)	Hombres (n =)
PAS normal	45	32
PAS elevada	15	28

La prueba de Pearson χ2 también puede usarse si tiene una tabla de 2x3 o 2x4, o incluso una de 3x3 o 6x8, siempre que tanto la variable dependiente como la independiente sean nominales u ordinales. Por ejemplo:

SEXO
	Mujeres(número, n=)	Hombres (n=)
PAS < 120 mmHg	33	18
PAS 120 - 139 mmHg	12	14
PAS ≥ 140 mmHg	15	28

EDAD (años)
PAS	30-39	40-49	50-59	60-69	≥70
PAS < 120	121	113	93	68	59
PAS 120-139	72	81	95	86	121
PAS ≥ 140	36	52	71	88	63

Dado que el análisis de χ2 solo se aplica para datos categóricos (nominales u ordinales), no es necesario estimar los promedios y, por lo tanto, no existen problemas con la distribución normal. Es por ello que no debemos preocuparnos por decidir si usar análisis paramétrico o no paramétrico. Con el análisis de Pearson χ2, el problema de la distribución de datos no se aplica.

Coeficiente Kappa de Cohen
Una estadística algo especial, en el sentido de que tiene una aplicación muy específica, es el coeficiente Kappa de Cohen. Es muy similar al análisis de Pearson χ2, ya que es una prueba para la cual tanto la variable dependiente como la independiente son categóricas. Donde difiere es que, mientras que con el análisis de Pearson χ2, la variable dependiente o independiente, o ambas, pueden ser ordinales, para calcular el coeficiente de Kappa, ambas deben ser nominales. Otra diferencia es que, a diferencia del análisis de χ2 de Pearson, solo puede utilizar una tabla de resultados de 2 x 2, y no las tablas de resultados de 2 x 3 o 5 x 3 dadas como ejemplos anteriores.
Lo que el análisis Kappa de Cohen prueba específicamente es si dos individuos (o, con menos frecuencia, grupos) ESTÁN DE ACUERDO con algo. Por ejemplo, ¿dos doctores diferentes presentan el mismo diagnóstico cuando examinan una serie de pacientes? ¿Se presentan dos laboratorios diferentes con el mismo resultado (un resultado anormal o un resultado normal) al probar una serie de muestras?
Como ya se ha dicho, el coeficiente de Kappa sólo permite usar una tabla n x n; específicamente, una tabla de 2 x 2, como se explicó anteriormente. Por ejemplo, si estaba probando si dos radiólogos diferentes están de acuerdo en que una imagen de rayos X determinada muestra un resultado normal o anormal en una serie de pacientes, generaría una tabla como la siguiente:

		Radiólogo A
		Normal	Anormal
Radiólogo B	Normal	25	5
	Anormal	10	40

El coeficiente de Kappa (representada como κ) se calcula esencialmente para reflejar las proporciones combinadas de radiografías leídas por ambos radiólogos como normales, versus las leídas por ambos radiólogos como anormales, y terminará siendo un número entre 0 (sin acuerdo) y 1,00 (acuerdo total). Un valor kappa κ=0,63 significa esencialmente que hubo un 63% de acuerdo, en general, entre los dos radiólogos.
Nótese que usted PODRÍA usar la prueba de Pearson χ2 con los mismos datos para generar una tabla como la que se muestra a continuación. Pero insertaría diferentes números (no los 25, 5, 10 y 40 que se muestran arriba). Por ejemplo, a partir de los números anteriores, sabemos que el radiólogo A calificó un total de 45 radiografías como anormales (40 de acuerdo con el radiólogo B y 5 en desacuerdo con el radiólogo B) y 35 de forma normal (25 de acuerdo con el radiólogo B y 10 en desacuerdo). Mientras tanto, usando la misma lógica, el radiólogo B calificó 50 radiografías como anormales y 30 como normales.

	Número de pacientes (n =) con radiografía calificada como normal	Número de pacientes (n =) con radiografía calificada como anormal
Radiólogo A	35	45
Radiólogo B	30	50

A partir de estos números, usted PODRÍA utilizar la prueba χ2 de Pearson y ver si los dos radiólogos son estadísticamente diferentes, pero esto no refleja el porcentaje de acuerdo entre ambos, lo cual sí es realizado con efectividad por el coeficiente Kappa de Cohen. ¿Podrían las dos pruebas valer la pena en un estudio dado? Sin duda, dependiendo de lo que usted quiera averiguar.
Por último, ¿Qué hacer si tiene MÁS DE DOS radiólogos o médicos que hacen un diagnóstico o laboratorios que proporcionan resultados a analizar? Para tales casos, hay otra prueba llamada Coeficiente Kappa de Fleiss, que funciona de la misma manera.

Prueba de la t de Student
La prueba de la t de Student compara esencialmente dos grupos de datos en función de una variable normalmente distribuida, como la PAS medida en mmHg o el peso medido en kilogramos. Volviendo al primer ejemplo sobre la presión arterial sistólica, sería una prueba muy apropiada usar una prueba de la t de Student: en el ejemplo a continuación, se estaría intentando determinar si el valor promedio de 145.7 es estadísticamente menor que el valor promedio de 153.2 mmHg.

	Grupo A	Grupo B
PAS	145.7 mmHg	153.2 mmHg

Tenga en cuenta que las pruebas de la t de Student pueden utilizarse para variables apareadas o no. Las pruebas no apareadas se utilizan cuando se comparan dos grupos, lo que se denomina una comparación entre grupos (por ejemplo, pacientes con fármaco activo vs. pacientes con placebo). Las pruebas apareadas se utilizan cuando se compara la misma variable en dos momentos diferentes en un grupo, lo que se denomina una comparación dentro del grupo (por ejemplo, antes o después del tratamiento). Una descripción más detallada de los análisis intergrupales versus intragrupales se proporcionó al principio de este trabajo.
A diferencia del análisis χ2, dado que las pruebas t, por su propia naturaleza, tratan con datos continuos, debe verificar si sus datos se distribuyen normalmente o no normalmente antes de seleccionar esta prueba. Si el caso fuera este último, se debe considerar usar una prueba no paramétrica, como la prueba de suma de rangos de Wilcoxen o la prueba U de Matt-Whitney.

Análisis de la Varianza (ANOVA)
El análisis de la varianza es muy parecido a una prueba t, excepto que está comparando MÁS de 2 grupos. Por ejemplo:

	Grupo A	Grupo B	Grupo C
PAS promedio	145.7	153.2	167.4
	mmHg	mmHg	mmHg

Existen variantes de ANOVA, como el análisis de la covarianza (ANCOVA), que compara una media variable continua entre> 2 grupos, y al mismo tiempo también se observa una covariable, como el género. Dicho de otra manera, si hay una diferencia entre los tres grupos, ¿puede explicarse sobre la base de las diferencias en un género frente a otro? Por ejemplo, considere que la PAS promedio a través de los tres grupos es casi idéntica en las mujeres (por ejemplo, 149.2, 150.0, 148.7 mmHg), pero bastante diferente en los hombres (por ejemplo, 143.9, 156.2, 171.8 mmHg).
Tenga en cuenta que, al igual que con las pruebas de la t de Student, los ANOVA pueden realizar comparaciones apareadas y no apareadas. Para comparaciones sin parear (por ejemplo, comparando tres o más grupos diferentes), ANOVA unidireccional o bidireccional funciona (dependiendo de si usted está mirando solo una o dos variables independientes categóricas).
Para los análisis apareados (por ejemplo, estudiando la misma variable varias veces a lo largo del tiempo), use el ANOVA de medidas repetidas, que es la "mejor manera" de comparar los grados de mejora en los diferentes grupos de tratamiento que la había prometido proporcionarle antes. Lo que ANOVA de medidas repetidas le permite hacer es comparar las medidas de resultado en múltiples momentos diferentes entre múltiples grupos diferentes, como en la Figura 5 a continuación.
En el ejemplo anterior, el ANOVA de medidas repetidas está analizando simultáneamente los efectos del tiempo y del grupo sujeto en la variable dependiente (p. Ej., Gravedad del dolor). Dados los resultados de la figura anterior, casi con certeza ambos efectos serían altamente significativos (p. Ej., P <0.001), disminuyendo claramente el dolor a lo largo del tiempo (especialmente en los tres grupos de tratamiento activo), pero también difiriendo entre los cuatro grupos de sujetos.
Independientemente del tipo de ANOVA que se realice (p. Ej., ANOVA de medidas repetidas versus ANOVA de una o dos vías), si se identifican efectos significativos, el siguiente paso sería realizar lo que se denomina una prueba post hoc para identificar cuáles grupos son diferente de cuáles otros. En el seguimiento de un mes en la Figura 5, por ejemplo, el nivel promedio de dolor entre aquellos pacientes que han recibido la tercera dosis (la más alta) del fármaco activo, sería sin duda menor que entre los que tomaron placebo. Quizás lo mismo sería cierto si se comparan las dosis 1 y 2 versus el placebo. Pero es poco probable que las dosis 1 y 2 difieran entre sí. Y el dolor reportado en esas dosis podría o no ser más alto que para la dosis 3. Las pruebas post-hoc aclararían todo esto. También se podrían realizar pruebas post-hoc para identificar las diferencias entre el estado basal (pre-tratamiento) y los diversos momentos en el tiempo en los que se han realizado controles del tratamiento (en el ejemplo, a 1, 3, 6 y 12 meses).
La prueba post-hoc más comúnmente usada es la prueba de Tukey, que se puede realizar en SPSS simplemente haciendo clic en la casilla "Prueba de Tukey" al configurar su ANOVA. Luego se hará automáticamente. Hay muchas otras pruebas post-hoc; pero recuerde sólo la prueba de Tukey y con eso debería ser suficiente para casi cualquier situación.
Al igual que con las pruebas de la t de Student, ANOVA (una prueba paramétrica) requiere la asunción de datos distribuidos normalmente. Por lo tanto, si sus datos no se distribuyen normalmente, no puede usar ANOVA.
Afortunadamente, además existir una prueba no paramétrica que se puede usar en lugar de una prueba de la t de Student para comparar dos grupos, también hay una prueba no paramétrica que se puede usar cuando hay más de dos grupos de asignaturas. Esta prueba no paramétrica de uso que compara más de dos grupos se denomina prueba de Kruskal-Wallis. Es similar a la prueba de Wilcoxen (una prueba no paramétrica para comparar dos grupos, descrita anteriormente), pero está diseñada específicamente para manejar MÁS de dos grupos. La Tabla 4, a continuación, resume todo esto.

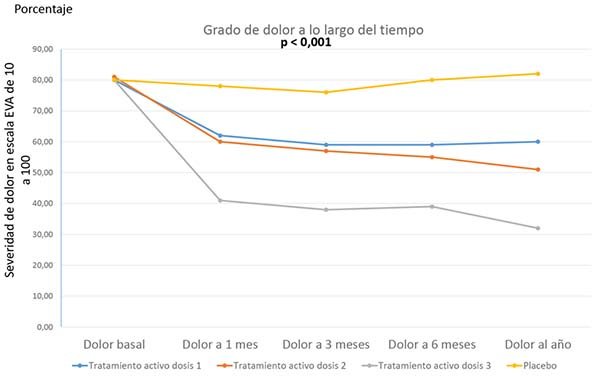
Figura 5.

Análisis de la correlación
El análisis de correlación busca ver si dos variables continuas están correlacionadas entre sí; en otras palabras, ¿alguna de las variables cambia de manera consistente en relación con los cambios la otra? Una manera simple de imaginar esto es hacer dos preguntas:

Si trazo las dos variables para cada sujeto en un gráfico, ¿qué tan bien conecta una línea los valores? Y
¿Tiene esta línea una pendiente positiva o negativa (es decir, una pendiente distinta de cero)?

Si la pendiente es positiva (cuando uno sube, el otro sube, como en la Figura 6, justo arriba), se dice que las variables están correlacionadas positiva o directamente; si la pendiente es negativa (a medida que una sube, la otra baja), se dice que se correlacionan negativa o inversamente. Las dos variables en el gráfico anterior están altamente correlacionadas directamente, con r=0,92 (máximo posible r=1,00).
El análisis de correlación de Pearson es la prueba de correlación más comúnmente utilizada. Esta prueba le arroja como resultado dos valores: un coeficiente de correlación (r) y un valor de p. Es crucial recordar que estos dos valores le dicen cosas muy diferentes. El valor de p le dice si las dos variables de interés están estadísticamente correlacionadas (si p <0.05, lo están); sin embargo, no le dice NADA sobre cuán fuerte es el grado de correlación. La fuerza de la correlación es lo que el valor de r le indica. Los valores r van de -1.00 a +1.00. Si r es mayor que +0.70, los dos valores generalmente se consideran fuertemente correlacionados positivamente (directamente). Si r está entre 0.50 y 0.70, la mayoría dirá que los dos valores están moderadamente correlacionados positivamente. Si r está entre 0.30 y 0.50, puede decir que la correlación es débil. Cualquier cosa por debajo de 0,30 se considera una correlación muy débil. Y lo mismo es cierto de los valores r negativos. Si r es menor que menos 0.70 (-0.70), las dos variables se correlacionan fuertemente negativamente (inversamente), y así sucesivamente.

Tabla 4: Comparando variables continuas entre dos versus más grupos

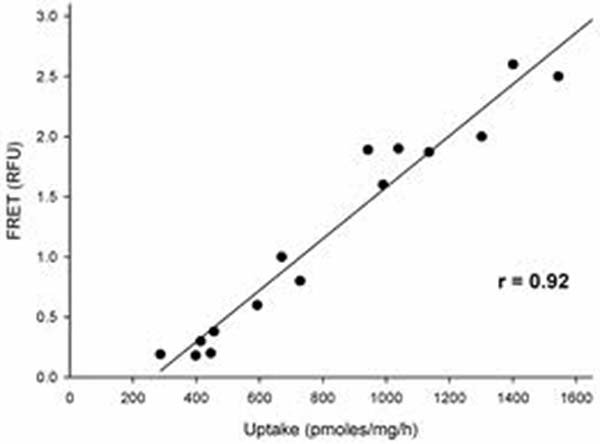
Figura 6: Una diagrama o trama de correlación.

Otra forma, aunque algo simplificada, de pensar en la diferencia entre los valores p y r en los análisis de correlación es ver cómo se reflejan en los diagramas o tramas de correlación (gráficos); como en la Figura 7, a continuación.
Los dos primeros gráficos (A y B) demuestran cómo se reflejan los valores de p cuando se representan datos dependientes e independientes continuos. Observe en A, para el cual el valor de p es <0.05, cómo todos los puntos de datos están muy cerca de la línea de la pendiente. Por el contrario, en la gráfica B, para la cual p es> 0.10 (lo que indica que no hay una correlación significativa), muchos de los puntos de datos están bastante alejados de la línea de la pendiente. En esta comparación, donde las dos líneas de pendiente son casi idénticas, el valor de p es en gran parte un reflejo de qué tan cerca están los datos de la línea de pendiente. La pendiente de esa línea, a su vez, es un indicador del valor de r.
Mientras tanto, los gráficos C y D muestran líneas de pendiente con pendientes muy diferentes, siendo positiva y considerablemente mayor en la gráfica D que en la gráfica C. Por lo tanto, el valor de r también es mayor en D que en C.
Hay un punto más para destacar sobre los valores r. Ocurre que r2 es la proporción de varianza en una variable que se explica por la otra. Entonces, si r=+0.50, esto significa que (0.50)2, o el 25% de la varianza en uno se explica por el otro. Es por eso que r=0.70 se considera un umbral para una fuerte correlación. Si r=0.70, significa que aproximadamente la mitad (49%) de la varianza en uno se explica por el otro. En la Figura 6, donde r=0.92, casi el 85% (84.6%) de la varianza en uno es explicada por el otro, lo que haría que la correlación representada allí tuviera una correlación muy fuerte. Para el diagrama 7C, anterior, r2 sería (0.15) 2=2%; para la gráfica D (arriba) r2=(0.40) 2=16%. En otras palabras, el porcentaje de varianza en el talle de calzado explicado por el tamaño del calzado sería del 2% y del 16% en los dos gráficos, respectivamente, el primero indicativo de una correlación muy débil y el último de una correlación débil.
Con respecto a la cuestión de la normalidad o no de los datos, es importante mencionar que los coeficientes de correlación de Pearson pueden calcularse para datos distribuidos normalmente o no normalmente, por lo que no se aplica el problema de las pruebas paramétricas y no paramétricas.
¡¡¡Cuidado!!! Tenga cuidado de NO usar livianamente la palabra 'correlación' en su discusión, documentos a publicar o solicitudes de subvención para becas, porque cualquiera que conozca de estadística pensará que ha hecho o está planeando hacer un análisis de correlación de Pearson, que SÓLO ES POSIBLE si tiene dos variables. En todas las demás instancias, en lugar de decir que dos cosas están correlacionadas, diga que están 'relacionadas', 'asociadas' o incluso 'vinculadas'. Por ejemplo, un historial de tabaquismo está asociado con (o relacionado con) un mayor riesgo de cáncer de pulmón. Pero dado que el tabaquismo y la presencia de cáncer de pulmón son variables binarias (sí/no), no se pueden correlacionar estadísticamente. (Pregunta: ¿qué prueba usaría para mostrar una asociación entre estas dos variables binarias? Consulte la respuesta en el cuadro de texto en el punto siguiente).

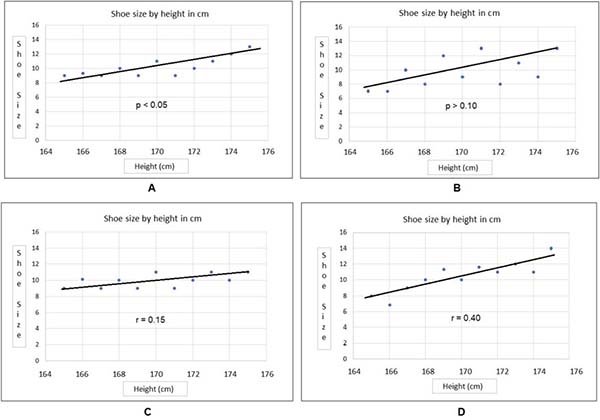
Figura 7: Exámenes de valores de p y r en tramas de correlación.

Análisis de la regresión
Mucha gente piensa que el análisis de la regresión es extremadamente complicado; sin embargo, realmente no lo es. Lo que permite un análisis de regresión es examinar si los cambios en una variable dependiente (ya sea continua, ordinal o nominal) pueden predecirse mediante cualquiera de una serie de otras variables. Por ejemplo, ¿puede predecirse la presión arterial sistólica según la edad, el peso y/o el sexo de una persona, y hasta qué punto? Al igual que el análisis de correlación, se generan valores R. Sin embargo, como son distintos de los valores r generados para el análisis de correlación, algunos prefieren llamarlos valores β (beta). Una gran ventaja del análisis de regresión sobre todas las otras pruebas discutidas en este trabajo, es que le permite examinar las influencias de un número considerable de variables independientes respecto una variable dependiente dada, en forma simultánea.
Si usted escribe una ecuación de regresión en papel, podría verse así:
PAS=(β1 x edad) + (β2 x peso) + (β3 x sexo) + β4

Respuesta a la pregunta realizada más arriba: la prueba más apropiada para usar con una variable binaria dependiente y otra independiente sería el análisis de Pearson χ2.

... donde β1, β2 y β3 son la magnitud de la influencia que cada una de las variables (edad, peso y sexo) tiene sobre la presión arterial sistólica, y β4 es el residuo no explicado por estas variables. El análisis de regresión es esencialmente solo 'resolver' para β1, β2 y β3 (en la ecuación anterior, β4 es la constante), al igual que solía resolver para x, y y z en matemáticas. Si recuerda de cuando usted estudiaba álgebra, podía resolver en una ecuación los valores de x, y y z, si tuviera tres ecuaciones separadas para cada variable. Por ejemplo: …

3x + 5y + 10z=12
5x - 2y - 7z=4
2x - 3y - 3z=4

Este ejemplo es particularmente sencillo, porque sólo juntando las tres ecuaciones, y y z desaparecen. Por lo tanto, usted termina con algo así: 10x=20, y por ende x=2. Luego se inserta el valor de 2 para x en dos de las ecuaciones para resolver y, y finalmente se procede en forma similar para z.
El análisis de regresión es esencialmente lo mismo que lo explicado arriba; excepto que, si tiene datos sobre 60 sujetos, tiene 60 ecuaciones que puede usar para estimar los valores de β1, β2, β3 y la constante β4. Este mayor número de ecuaciones le permite no solo determinar cuáles son los valores de β1, β2, β3 y β4, sino también determinar si alguno de estos valores es estadísticamente diferente de cero. Si, por ejemplo, los límites de confianza del 95% para β1 se superponen a cero (p. Ej., -0.21≤β≤+0.39), la variable independiente asociada con β1 (del ejemplo anterior, edad) no tiene un efecto estadísticamente significativo en la PAS. Por otro lado, si los límites de confianza para β1 NO se solapan estadísticamente con cero (p. Ej., +0.06≤β≤+0.52), se supone que la edad ha ejercido cierta influencia sobre la PAS; y el tamaño y la dirección (directa o inversa) de esa influencia estará determinada por la magnitud y el signo (+ o -) de β1. Y así sucesivamente, para cada otra variable independiente (para β2, β3...) de su ecuación.
Tenga en cuenta que hay diferentes tipos de análisis de regresión, en función de si su variable dependiente es nominal, ordinal o continua. El análisis de regresión lineal se usa cuando la variable dependiente (como la presión arterial sistólica) es una variable continua. El análisis de regresión ordinal se usa si la variable dependiente es ordinal (por ejemplo, trabajar a tiempo completo, trabajar a tiempo parcial, no trabajar). El análisis de regresión logística se usa si la variable dependiente es tanto nominal como binaria (p. Ej., Enfermedad presente=1, enfermedad ausente=0): y se usa el análisis de regresión multinomial si su variable es nominal, pero tiene más de dos categorías (por ejemplo, caucásica, afroamericano, hispano, otro). La Tabla 5 resume todo esto.
Permítame establecer un punto crucial más sobre el análisis de regresión, que esencialmente se aplica a todas sus formas descriptas aquí. El punto es el siguiente: generalmente se requieren de 10 a 15 sujetos -por variable independiente probada- como para tener suficiente poder estadístico y de esa manera obtener un valor estadísticamente significativo.
Digamos por ejemplo que usted que desea identificar predictores potenciales de la supervivencia a un año después de un accidente cerebrovascular. Dado que la muerte versus supervivencia es una variable binaria (existen sólo dos opciones: el paciente vivió o el paciente murió), es necesario realizar una regresión logística, con 'sobrevivió/murió' (sobrevivió=1, murió=0) como su variable dependiente. Si las variables independientes que quería probar en el modelo incluían la edad del paciente, el sexo del paciente, la presencia/ausencia de enfermedad comórbida, antecedentes familiares de accidente cerebrovascular, presión arterial sistólica, presión arterial diastólica, otras enfermedades cardiovasculares, diabetes y cuatro características del accidente cerebrovascular en sí (por ejemplo, el grado de parálisis, alteraciones del habla +/-), usted estaría manejando doce variables independientes de interés, lo que significaría que necesita un mínimo de 120 sujetos, pero preferiblemente 180 o más para tener suficiente poder estadístico como para obtener un resultado estadísticamente significativo.
¿Pero qué se puede hacer si usted sólo posee 80 sujetos en estudio?
La respuesta sería realizar un análisis de regresión de tipo jerárquico (o paso a paso) que, en el caso de una variable logística binaria como 'sobrevivió/murió', sería un análisis de regresión logística binaria jerárquico. Para ello, comience ingresando sólo unas pocas variables en el modelo (por ejemplo, edad del paciente, sexo del paciente, historial familiar) y vea cuáles permanecen como predictores significativos de supervivencia, como primer paso. Digamos que la edad del paciente permanece en el modelo. Para el paso 2, cree un segundo modelo, ingrese la edad del paciente y otras tres variables, por ejemplo, comorbilidades, enfermedad cardiovascular, diabetes, y vuelva a probar el modelo para ver qué variables permanecen... y así sucesivamente hasta que haya ingresado cada variable independiente de interés al menos una vez. Una advertencia es que dos variables que esencialmente miden lo mismo (p. Ej., PAS medida con un manguito de presión arterial, PAS medida con un catéter intraarterial) PUEDEN anularse mutuamente; por lo tanto, no ingrese dichas variables juntas.
Finalmente, concluiré esta sección refiriéndome a las pruebas que usted tiene disponibles en el caso de que sus datos NO estén normalmente distribuidos (es decir, no poseen una forma de campana al graficarlos) por lo cual deberá utilizar pruebas no paramétricas.

Variable dependiente	Ejemplo(s)	Prueba estadística
Continua	PAS; dolor en una escala de 0 a 100; sobrevida en meses	Regresión lineal simple
Ordinal	Retorno al trabajo (tiempo completo, tiempo parcial, no retorno)	Regresión ordinal
Multinomial	Ciudad de residencia (Buenos Aires, Lima, Madrid, Nueva York)	Regresión multinomial
Binaria	ACV/no ACV; muerte/sobrevida ; fumador/no fumador	Regresión binaria logística

Pruebas no paramétricas (de rango)
No se preocupe demasiado por las pruebas de rango: sólo es importante conocer que también se llaman pruebas no paramétricas, y se utilizan siempre que una variable dependiente continua u ordinal no se distribuye normalmente. Las más utilizadas son la prueba de suma de rangos de Wilcoxen y la prueba U de Mann-Whitney, para usar cuando tiene dos grupos de sujetos, y la prueba H de Kruskal-Wallis cuando tiene más de dos grupos de sujetos.
En otras palabras, si desea hacer una prueba t de Student, pero durante el análisis de datos descubre que ello no es posible debido a que sus datos no se distribuyen normalmente, realice la prueba de suma de rangos de Wilcoxen o la prueba U de Mann-Whitney. Si, por otro lado, planeaba realizar ANOVA, pero no puede hacerlo porque sus datos no se distribuyen normalmente, seleccione la prueba H de Kruskal-Wallis. Todo esto se resumió sucintamente en la Tabla 4.
Un ejemplo de cómo se clasifican las mediciones (explicado anteriormente en este artículo) se repite aquí. En ese ejemplo, se midió la presión arterial sistólica (PAS) en todos los sujetos en dos grupos, pero los datos no se distribuyeron normalmente. Para compensar esto, en lugar de calcular la PAS promedio para los dos grupos, todas las lecturas individuales se clasificaron, de mayor a menor, como se muestra en la tabla a continuación:
Observe nuevamente cómo un rango, desde la PAS más alta a la más baja, se proporciona entre paréntesis al lado de cada medición, y cada rango se encuentra en todo el conjunto de datos (ambos grupos de sujetos).

Grupo A: PAS (rango)	Grupo B: PAS (rango)
183 (2)	185 (1)
162 (4)	178 (3)
150 (6)	152 (5)
145 (8)	146 (7)
138 (9)	126 (11)
128 (10)	125 (12)
110 (14)	114 (13)
108 (15)	106 (16)

Las pruebas de rango utilizan estas clasificaciones para identificar si los dos grupos son diferentes, en lugar de promedios grupales. Y eso es todo lo que creo que la mayoría de la gente necesita saber sobre las pruebas no paramétricas.

Resumiendo, las pruebas
La tabla 6 resume las diferentes pruebas que han sido descriptas en este artículo.
Note usted que, debido a que es muy específico, he excluido deliberadamente el coeficiente Kappa de Cohen de la tabla anterior. Para revisar este punto, puede dirigirse al apartado específico referido a esta prueba, más atrás.

DÁNDOLE SENTIDO A LOS RESULTADOS

La quinta y última regla que le daré, seguramente a esta altura ya la sabe:

Regla #5: Generalmente, p=0.05 se establece como umbral para la significancia estadística.

Pero, ¿qué significa esto realmente?
Al informar los valores p, tenga en cuenta que un valor p de 0.04 significa que está 96% seguro de que hay una diferencia entre los grupos. Un valor p de 0.001 significa que está 99.9% seguro. Obviamente, p <0.05 significa que tiene MÁS del 95% de certeza de que la diferencia que ha detectado es real.
Tiene poco sentido reportar que un valor p es 0.00023. Cualquier cosa menor que 0.001 sólo debe informarse como p <0.001. Si tiene más del 99.9% de certeza de algo, es MÁS que suficiente para ser informado. No es necesario decir que usted posee un 99.99977% de certeza. Además, a menos que tenga una enorme muestra de sujetos (por ejemplo, una encuesta clínica o de población general de más de 1000 sujetos), es casi seguro que no tenga los números que justifiquen la presentación de ALGO MÁS ALLÁ de 2 o 3 decimales.
En algún momento, puede escuchar que un valor de p se ajusta para comparaciones múltiples.

Tabla 6: Un resumen de las pruebas estadísticas más comunes

Prueba estadística	Variable dependiente	Variable independiente	Número de grupos	Distribución de datos	Estadístico de prueba
Prueba de la t de Student	Continua	Categórica*		Normal	t
ANOVA	Continua	Categórica*	Más de 2	Normal	f
Pearson χ2	Categórica	Categórica*	Cualquier número	n/a	χ2
Análisis de la correlación de Pearson	Continua	Continua	n/a	n/a	r, r2 **
Análisis de la regresión	Ya sea***	Todas****	n/a	n/a	β, R, R2
Prueba de suma de rangos de Wilcoxen	Continua u ordinal	Categórica*	2	No-normal	W1 & W2
Prueba de la U de Mann-Whitney	Continua u ordinal	Categórica*	2	No-normal	U1 & U2
Prueba H de Kruskal-Wallis	Continua u ordinal	Categórica*	Más de 2	No-normal	χ2

* Categórica = nominal u ordinal. **r2 = es el porcentaje de la varianza de una variable predicha por la otra variable. *** Si la variable dependiente es binaria, realizar una regresión logística; si es multinomial, una regresión multinomial; si es continua, una regresión lineal simple; y si es ordinal, una regresión ordinal. **** Variables nominales, ordinales o continuas, todas pueden ser incluidas dentro del mismo modelo de regresión.

Esto es lo que eso significa. Si establece su umbral de significancia estadística como p <0.05, cualquier valor de p por debajo de 0.05 indica que está más de 95% seguro de que su conclusión es correcta. Sin embargo, esto significa conceder que, cuando p=0.05, también hay un 5% de posibilidades de que la conclusión que ha dibujado sea incorrecta. De hecho, una de cada 20 pruebas, en promedio, será un falso positivo, puramente por casualidad.
Considere ahora que está haciendo veinte pruebas estadísticas dentro de un estudio dado. Estadísticamente, por casualidad, una de estas veinte pruebas debería arrojar un resultado incorrecto. Esto podría ser un resultado falso positivo (identifica una diferencia entre dos grupos cuando no existe una diferencia verdadera, el denominado error de tipo 1), o un resultado falso negativo (no se identifica una diferencia entre dos grupos cuando los dos grupos son realmente diferentes, llamado error tipo 2). De cualquier manera, estableciendo su umbral de valor de p para significancia estadística como p <0.05, teóricamente llegará a una conclusión incorrecta una vez cada veinte pruebas. Y esa prueba podría ser la más importante (es decir, su resultado principal).
¿Cómo manejar este problema?
La respuesta es muy simple: configure su umbral de p para significancia estadística en algún valor menor que 0.05. Si, por ejemplo, lo establece como p <0.01, esto significa que está 99% seguro de que un resultado dado es exacto, lo que significa que cree que hay solo un 1% de probabilidad de que una conclusión dada sea incorrecta. Si establece el umbral de p como 0.02, estaría 98% seguro, 2% inseguro, y teóricamente solo esperaría un resultado erróneo en 50 pruebas.
Una manera formal y muy estricta de ajustar la p para comparaciones múltiples es dividir el umbral p estándar, de 0.05, por el número de pruebas que planea realizar. Por ejemplo, si realiza 10 pruebas, divida 0.05 por 10, lo que le da un nuevo umbral para la significación estadística de p <0.005. Con este umbral de valor p, debe tener 99.5% de certeza y solo 0.5% de incertidumbre sobre cada resultado. Por lo tanto, sería 10 x 0.05%, o 5% seguro de que TODAS sus conclusiones son correctas.
Este método de ajustar su valor de p, dividiendo 0.05 por el número de comparaciones estadísticas que tiene la intención de hacer, se denomina ajuste de Bonferroni para comparaciones múltiples.
Y este es un resumen rápido y básico de las estadísticas médicas. ¡Espero sea de su utilidad!